In High Performance Computing everything counts. Martin Thompson (former LMAX CTO) warns us in his excellent talks and blog about the cost of the division operation in the modern CPUs.
The division operation is performed by a specific unit. In Intel Sandy Bridge microprocessor only one DIV unit is available, while there are multiple ALU units (arithmetic logic unit) for the rest of the Maths.
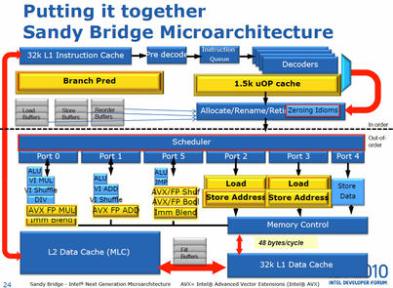
The cost of accessing this unit it appears to be higher than the other operations. Very often the division is used to calculate the reminder to find the next available position in a ring buffer, or activate a bit in a bloom filter or find the right partition in a hash distribution.
Martin suggests a more efficient way to calculate the reminder using bitwise operation.
First of all some limitations. This can be done only if the divisor or denominator is a power of 2. This limitation shouldn’t be a problem as in most of the cases we control the size of the ring buffer or hash structure.
Let’s assume that our divisor is d (and it is a power of 2), if we want to calculate the reminder of n as n % d = r then we have to proceed in the following way:
mask = d - 1
r = n AND mask
or simply
r = n AND (d-1)
to see how it works assume that d = 8 (–> in binary 01000) then assume we want to find the reminder of the following numbers 25, 63 and 155
7 6 5 4 3 2 1 0 bits
| | | | | | | | |
1 1 0 0 1 = 25
1 1 1 = 7 --> MASK (8-1)
0 0 1 = 1 --> 25 & (8-1) == 1
7 6 5 4 3 2 1 0 bits
| | | | | | | | |
1 1 1 1 1 1 = 63
1 1 1 = 7 --> MASK (8-1)
1 1 1 = 7 --> 63 & (8-1) == 7
7 6 5 4 3 2 1 0 bits
| | | | | | | | |
1 0 0 1 1 0 1 1 = 155
1 1 1 = 7 --> MASK (8-1)
0 1 1 = 3 --> 155 & (8-1) == 3
As seen with a single and efficient bit operation (AND) we get our reminder. Finally I’ve run some benchmarks to verify the result:
and the result on my Intel iCore7 laptop is:
$ java ReminderBenchmark 10000
average bitwise = 795684
average division = 2134931
So it looks like is ~3 times faster than the reminder operator.
